Statistical Mechanics 2



Leo Lue

Department of Chemical & Process Engineering

University of Strathclyde

Review

  • thermodynamics
    entropy: \(S(N,V,E)\)
    At fixed \(N\), \(V\), and \(E\), the entropy of a system is maximized at equilbrium.
  • microscopic dynamics
    density of states: \(\Omega(N,V,E)\)
  • connection
    \(S(N,V,E) = k_B \ln \Omega(N,V,E)\)
    where \(k_B=1.3806503\times10^{-23}\) J K\(^{-1}\) is the Boltzmann constant

Phase space

Your browser does not support SVG

Density of states

  • The density of states \(\Omega(N,V,E)\) is the number of ways the system can have an energy \(E\). In other words, it is the "volume" of phase space with an energy \(E\).

  • Mathematically, the density of states is given by

    \begin{equation*} \Omega(N,V,E) = \int_{E < H({\boldsymbol\Gamma})< E+\delta E} d{\boldsymbol\Gamma} \end{equation*}

    where \(\delta E\ll E\).

  • Volume element in phase space:

    \begin{equation*} d{\boldsymbol\Gamma} = \frac{1}{N!} \frac{d{\bf r}_1d{\bf p}_1}{h^3}\cdots \frac{d{\bf r}_N d{\bf p}_N}{h^3} \end{equation*}

    where \(h\) is Planck's constant.

Basic concepts

Consider one microscopic state \(\boldsymbol{\Gamma}\) out of the \(\Omega(N,V,E)\) microscopic states. The probability of its being occupied is:

\begin{equation*} {\mathcal P}({\boldsymbol\Gamma}) \propto \frac{1}{\Omega(N,V,E)} \end{equation*}

In the \(NVE\) ensemble, we can now determine average properties if the density of states, \(\Omega(N,V,E)\) is known.

\begin{align*} \langle{\mathcal A}\rangle &= \int {\rm d}{\boldsymbol\Gamma}\,{\mathcal P}({\boldsymbol\Gamma})\, {\mathcal A}({\boldsymbol\Gamma}) = \lim_{t_{\rm obs}\to\infty} \frac{1}{t_{\rm obs}} \int_0^{t_{\rm obs}} {\rm d}t\,{\mathcal A}({\boldsymbol\Gamma}(t)) \end{align*}

Overview

  • microcanonical ensemble: \(NVE\)
  • canonical ensemble: \(NVT\)
  • isothermal-isobaric ensemble: \(NpT\)
  • fluid structure
  • summary

Microcanonical ensemble

\begin{align*} S(N,V,E) &= k_B \ln \Omega(N,V,E) \end{align*}

Fundamental equation of thermodynamics:

\begin{align*} {\rm d}S(N,V,E) &= - \frac{\mu}{T}{\rm d}N + \frac{p}{T}{\rm d}V + \frac{{\rm d}E}{T} \\ {\rm d}\ln\Omega(N,V,E) &= - \beta\,\mu\,{\rm d}N + \beta\,p\,{\rm d} V + \beta\,{\rm d}E \end{align*}

where \(\beta=1/(k_B\,T)\).

\begin{align*} \frac{\partial\ln\Omega(N,V,E)}{\partial N} = -\beta\mu; \qquad \frac{\partial\ln\Omega(N,V,E)}{\partial V} = -\beta p; \qquad \frac{\partial\ln\Omega(N,V,E)}{\partial E} = \beta \end{align*}

At fixed \(N\), \(V\), and \(E\), \(\Omega(N,V,E)\) is maximized at equilibrium. Once the density of states \(\Omega(N,V,E)\) is known, all the thermodynamic properties of the system can be determined.

Example: lattice of two state sites

  • \({\mathcal N}\) lattice sites
  • Each lattice site has two states: state \(0\) with energy \(0\), and state \(1\) with energy \(\varepsilon\)
  • If \(n_0\) is the number of sites in state \(0\), and \(n_1\) is the number of sites in state \(1\), the total energy of the system is \(E=n_1\varepsilon\). Note \(n_0+n_1={\mathcal N}\).

  • density of states:

    \begin{align*} \Omega(E) = \frac{{\mathcal N}!}{(E/\varepsilon)!({\mathcal N}-E/\varepsilon)!} \end{align*}

thermal equilibrium

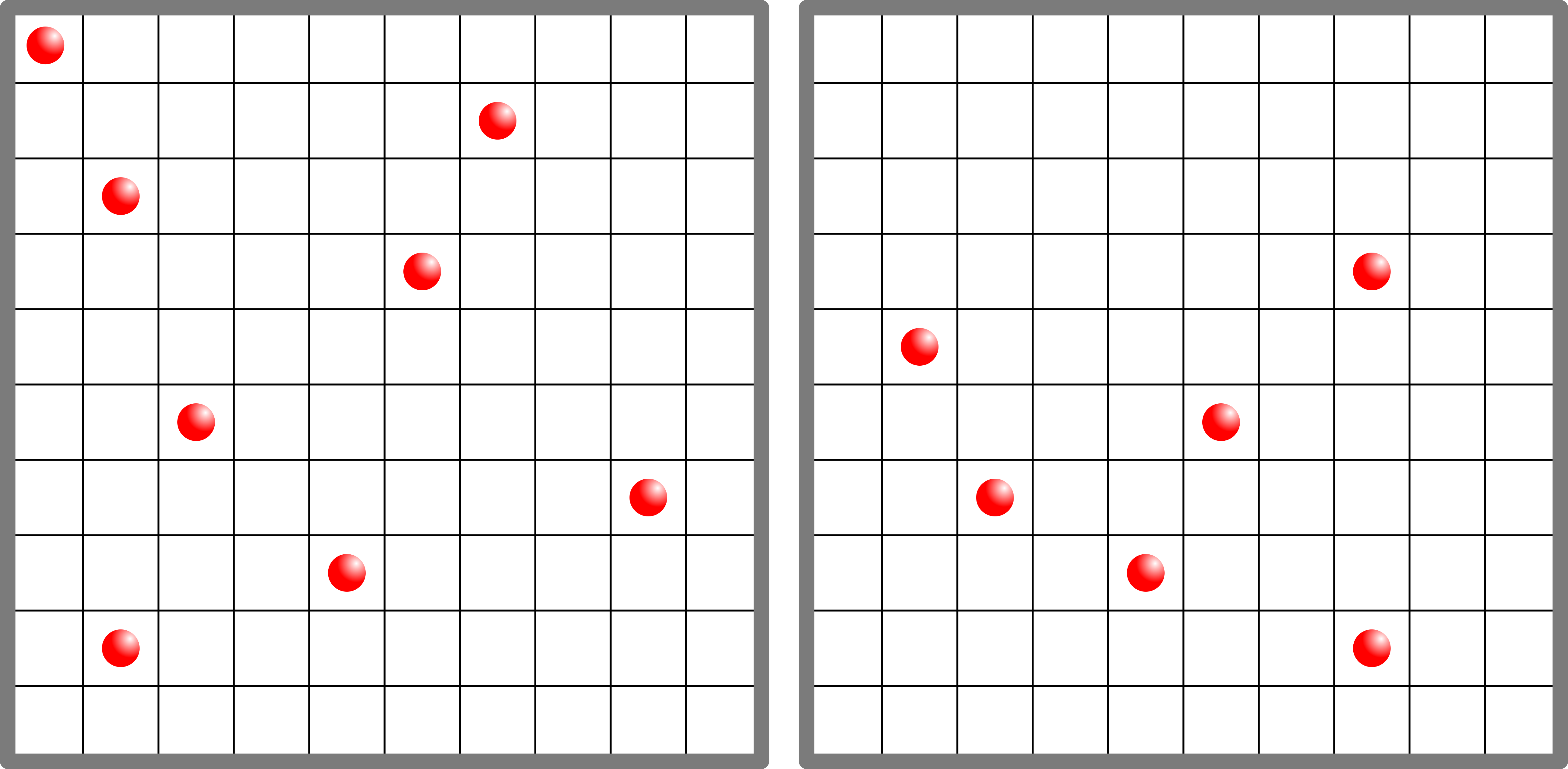
  • energy: \(E=E_A+E_B\)
  • density of states: \(\Omega_{A+B}(E)=\Omega_A(E_A)\Omega_B(E_B)\)
  • entropy: \(S_{A+B}(E)=S_A(E_A)+S_B(E_B)\)

Canonical ensemble

Your browser does not support SVG
\begin{equation*} {\mathcal P}(E) \propto \Omega(E;E_{\rm tot}) \qquad \qquad \Omega(E;E_{\rm tot}) = \Omega(E) \Omega_{\rm surr} (E_{\rm tot}-E) \end{equation*}

(Note: the \(N\) and \(V\) variables for the system and the surroundings are implicit)

Canonical ensemble

\begin{align*} {\mathcal P}(E,E_{\rm tot}) &\propto \Omega(E) \Omega_{\rm surr}(E_{\rm tot}-E) \\ &\propto \Omega(E) e^{\ln \Omega_{\rm surr}(E_{\rm tot}-E)} \end{align*}

Performing a Taylor expansion of \(\ln\Omega_{\rm surr}\) around \(E_{\rm tot}\).

\begin{align*} {\mathcal P}(E,E_{\rm tot}) &\propto \Omega(E) e^{\ln \Omega_B(E_{\rm tot}) - E \frac{\partial}{\partial E_{\rm tot}}\ln \Omega_B(E_{\rm tot}) + \cdots} \end{align*}

First-order is fine as \(E\ll E_{tot}\). Note that \(\partial \ln \Omega(E) / \partial E=\beta\). At equilibrium the surroundings and system have the same temperature thus:

\begin{align*} {\mathcal P}(E,E_{\rm tot}) &\propto \Omega(E) e^{\ln \Omega_B(E_{\rm tot}) - \beta E} \end{align*}
\begin{align*} {\mathcal P}(E) &\propto \Omega(E) e^{- \beta E} \end{align*}

(If the surroundings are large, \(E_{\rm tot}\) is unimportant and the constant term \(\ln \Omega_B(E_{\rm tot})\) cancels on normalization)

Canonical ensemble

  • Boltzmann distribution

    \begin{equation*} {\mathcal P}(E) = \frac{\Omega(N, V, E)}{Q(N,V,\beta)} e^{ - \beta\,E} \end{equation*}

  • partition function is the normalization:

    \begin{equation*} Q(N,V,\beta) = \int {\rm d}E\,\Omega(N,V,E) e^{-\beta\,E} \end{equation*}

average energy

\begin{align*} \langle E\rangle &= \int dN\,dV\,dE\, E\, {\mathcal P}(N,V,E) \\ &= \int dN\,dV\,dE\, E\, \frac{\Omega(N, V, E)}{Q(N,V,\beta)} e^{ - \beta\,E} \\ &= \int dN\,dV\,dE\, \frac{\Omega(N, V, E)}{Q(N,V,\beta)} \left[ -\frac{\partial}{\partial\beta}e^{ - \beta\,E}\right] \\ &= - \frac{1}{Q(N,V,\beta)} \frac{\partial}{\partial\beta} \int dN\,dV\,dE\, \Omega(N, V, E)\, e^{ - \beta\,E} \\ &= - \frac{1}{Q(N,V,\beta)} \frac{\partial Q(N,V,\beta)}{\partial\beta} \\ &= - \frac{\partial}{\partial\beta} \ln Q(N,V,\beta) \end{align*}

volume derivative

\begin{align*} \frac{\partial}{\partial V} \ln Q(N,V,\beta) &= \frac{1}{Q(N,V,\beta)} \int dN\,dV\,dE\, \frac{\partial\Omega(N,V,E)}{\partial V} e^{-\beta\,E} \\ &= \frac{1}{Q(N,V,\beta)} \int dN\,dV\,dE\, \frac{\partial\ln\Omega(N,V,E)}{\partial V} \Omega(N,V,E)\, e^{-\beta\,E} \\ &= \int dN\,dV\,dE\,\beta p(N,V,E) \frac{\Omega(N,V,E)}{Q(N,V,\beta)} e^{-\beta\,E} \\ &= \int dN\,dV\,dE\,\beta p(N,V,E)\, {\mathcal P}(N,V,E) \\ &= \beta p \end{align*}

number derivative

\begin{align*} \frac{\partial}{\partial N} \ln Q(N,V,\beta) &= \frac{1}{Q(N,V,\beta)} \int dN\,dV\,dE\, \frac{\partial\Omega(N,V,E)}{\partial N} e^{-\beta\,E} \\ &= \frac{1}{Q(N,V,\beta)} \int dN\,dV\,dE\, \frac{\partial\ln\Omega(N,V,E)}{\partial N} \Omega(N,V,E)\, e^{-\beta\,E} \\ &= \int dN\,dV\,dE\,\beta [-\beta\mu(N,V,E)] \frac{\Omega(N,V,E)}{Q(N,V,\beta)} e^{-\beta\,E} \\ &= - \int dN\,dV\,dE\,\beta\mu(N,V,E)\, {\mathcal P}(N,V,E) \\ &= -\beta \mu \end{align*}

Helmholtz free energy

  • free energy

    \begin{align*} \beta A(N,V,T) &= - \ln Q(N,V,\beta) \end{align*}

  • derivative relations

    \begin{align*} {\rm d}A &= -S\,{\rm d}T -p\,{\rm d}V + \mu\,{\rm d}N \\ {\rm d}\ln Q(N,\,V,\,\beta) &= - E\,{\rm d}\beta + \beta\,p\,{\rm d}V - \beta\,\mu\,{\rm d}N \end{align*}

Again, all thermodynamic properties can be derived from \(Q(N,\,V,\,\beta)\).

Fluctuations

\begin{align*} \langle E^2\rangle &= \int dN\,dV\,dE\, E^2\, {\mathcal P}(N,V,E) \\ &= \int dN\,dV\,dE\, E^2\, \frac{\Omega(N, V, E)}{Q(N,V,\beta)} e^{ - \beta\,E} \\ &= \int dN\,dV\,dE\, \frac{\Omega(N, V, E)}{Q(N,V,\beta)} \left[\frac{\partial^2}{\partial\beta^2}e^{ - \beta\,E}\right] \\ &= \frac{1}{Q(N,V,\beta)} \frac{\partial^2}{\partial\beta^2} \int dN\,dV\,dE\, \Omega(N, V, E)\, e^{ - \beta\,E} \\ &= \frac{1}{Q(N,V,\beta)} \frac{\partial^2 Q(N,V,\beta)}{\partial\beta^2} \\ &= \frac{\partial^2}{\partial\beta^2} \ln Q(N,V,\beta) + \left[\frac{\partial}{\partial\beta}\ln Q(N,V,\beta)\right]^2 \\ &= \frac{\partial^2}{\partial\beta^2} \ln Q(N,V,\beta) + \langle E\rangle^2 \end{align*}

Energy fluctuations:

\begin{align*} \langle (E-\langle E\rangle)^2\rangle &= \frac{\partial^2}{\partial\beta^2} \ln Q(N,V,\beta) \\ \beta^2 \langle (E-\langle E\rangle)^2\rangle &= \frac{C_V}{k_B} \end{align*}

Partition function: density of states

\begin{align*} Q(N,V,\beta) &= \sum_{E} \Omega(N,V,E)\,e^{-\beta E} \end{align*}

The canonical partition function can be written in terms of an integral over phase space coordinates:

\begin{align*} Q(N,V,\beta) &= \int dE \Omega(N,V,E) e^{-\beta E} \\ &= \int dE e^{-\beta E} \int_{E \lt H({\boldsymbol\Gamma})\lt E+\delta E} d{\boldsymbol\Gamma} \\ &= \int d{\boldsymbol\Gamma}\, e^{-\beta H({\Gamma})} \\ &= \frac{1}{N!}\int \frac{d{\bf r}_1d{\bf p}_1}{h^3} \cdots \frac{d{\bf r}_N d{\bf p}_N}{h^3} e^{-\beta H({\Gamma})} \end{align*}

Factorization of the partition function

  • The partition function can be factorized: For \(H=U+K\)

    \begin{align*} Q(N,V,T) = \frac{1}{N!} \int d{\bf r}_1\cdots d{\bf r}_N e^{-\beta U({\bf r}_1,\dots{\bf r}_N)} \int \frac{d{\bf p}_1}{h^3}\cdots\frac{d{\bf p}_N}{h^3} e^{-\beta K({\bf p}_1,\dots,{\bf p}_N)} \end{align*}

  • The integrals over the momenta can be performed exactly

    \begin{align*} \int\frac{{\rm d}{\bf p}_1}{h^3}\cdots\frac{{\rm d}{\bf p}_N}{h^3} e^{-\beta K({\bf p}_1,\dots,{\bf p}_N)} &= \left[\int\frac{{\rm d}{\bf p}}{h^3} e^{-\frac{\beta\,p^2}{2\,m}} \right]^{N} \\ &= \left(\frac{2\,\pi\,m}{\beta h^2}\right)^{3\,N/2} = \Lambda^{-3\,N} \end{align*}

  • The partition function is given in terms of a configurational integral and the de Broglie wavelength \(\Lambda\)

    \begin{equation*} Q(N,\,V,\,T) = \frac{1}{N!\Lambda^{3\,N}} \int {\rm d}{\bf r}_1\cdots {\rm d}{\bf r}_N e^{-\beta\,U({\bf r}_1,\dots{\bf r}_N)} = \frac{Z(N,\,V,\,T)}{N!\Lambda^{3\,N}} \end{equation*}

Average properties

  • The probability of being at the phase point \({\boldsymbol\Gamma}\) is

    \begin{equation*} {\mathcal P}({\boldsymbol\Gamma}) = \frac{e^{-\beta\,H({\boldsymbol\Gamma})}}{Q(N,\,V,\,\beta)} \end{equation*}

  • The average value of a property \({\mathcal A}({\boldsymbol\Gamma})\) is

    \begin{align*} \langle{\mathcal A}\rangle &= \int {\rm d}{\boldsymbol\Gamma} {\mathcal P}({\boldsymbol\Gamma}) {\mathcal A}({\boldsymbol\Gamma}) \\ &= \frac{1}{Q(N,\,V,\,\beta)}\int {\rm d}{\boldsymbol\Gamma} e^{-\beta H({\boldsymbol\Gamma})} {\mathcal A}({\boldsymbol\Gamma}) \end{align*}

  • If the property depends only on the position of the particles

    \begin{align*} \langle{\mathcal A}\rangle &= \frac{1}{Q(N,V,\beta)} \int d{\bf r}_1\cdots d{\bf r}_N e^{-\beta U({\bf r}_1,\dots,{\bf r}_N)} {\mathcal A}({\bf r}_1,\dots,{\bf r}_N) \end{align*}

Boltzmann distribution

\begin{align*} P(E) \propto e^{-\beta E} \end{align*}

example: Barometric formula

Ideal gas at temperature \(T\) in a gravitational field.

Potential energy of gas molecule of mass \(m\) at height \(h\) is

\begin{equation*} E(h) = mgh \end{equation*}

Probability \({\mathcal P}(h)\) that a molecule is at height \(h\)

\begin{equation*} {\mathcal P}(h) \propto e^{-\beta E(h)} = e^{-\beta mgh} \end{equation*}

Concentration and pressure profile:

\begin{align*} c(h) &= c_0 e^{-\beta m g h} \\ p(h) &= p_0 e^{-\beta m g h} \end{align*}

where \(c_0\) is the concentration at \(h=0\), and \(p_0\) is the pressure.

example: Maxwell-Boltzmann velocity distribution

  • Kinetic energy:

    \begin{equation*} E({\bf v}) = \frac{m}{2} v^2 \end{equation*}

    where \(v^2=v_x^2+v_y^2+v_z^2\) is the particle speed.

  • Velocity distribution:

    \begin{align*} P({\bf v}) d{\bf v} &= (2\pi \beta m)^{-3/2} e^{-\beta m v^2/2} d{\bf v} \\ &= (2\pi \beta m)^{-3/2} e^{-\beta m v_x^2/2-\beta m v_y^2/2-\beta m v_z^2/2} dv_x dv_y dv_z \\ &= f(v_x) dv_x f(v_y) dv_y f(v_z) dv_z \end{align*}

Maxwell-Boltzmann velocity distribution

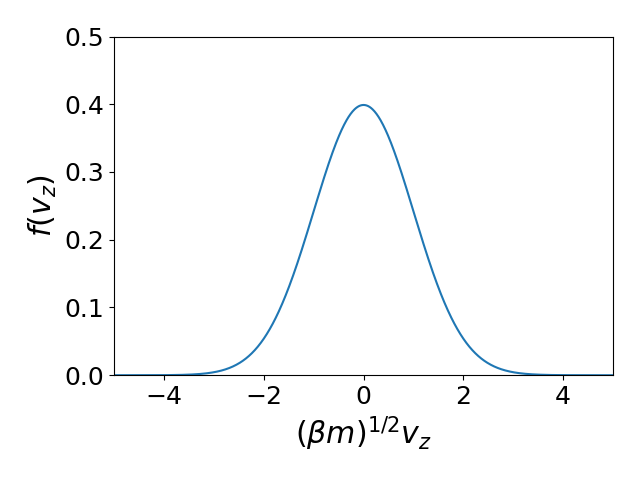
\begin{align*} f(v_z) = (2\pi \beta m)^{-1/2} e^{-\beta m v_z^2/2} \end{align*}

Maxwell-Boltzmann speed distribution

Speed distribution:

\begin{equation*} F(v) dv = (2\pi \beta m)^{-3/2} e^{-\beta m v^2/2} 4\pi v^2 dv \end{equation*}

Grand canonical ensemble

Your browser does not support SVG
\begin{align*} {\mathcal P}(N,E) &\propto \Omega(N,E;N_{\rm tot},E_{\rm tot}) \\ \Omega(N,E;N_{\rm tot},E_{\rm tot}) &= \Omega(N,E) \Omega_B(N_{\rm tot}-N,E_{\rm tot}-E) \end{align*}

Grand canonical ensemble

  • Boltzmann distribution

    \begin{equation*} {\mathcal P}(E,N) = \frac{\Omega(N, V, E)}{Z_G(\mu,V,\beta)} e^{\beta \mu N - \beta E} \end{equation*}

  • partition function

    \begin{equation*} Z_G(\mu, V, \beta) = \sum_{N} \int {\rm d}E\,\Omega(N,V,E) e^{\beta\,\mu\,N - \beta\,E} \end{equation*}

  • free energy

    \begin{align*} \Omega &= - pV = -k_BT \ln Z_G(\mu,V,\beta) \\ d\Omega &= - d(pV) = -S dT - pdV - N d\mu \\ d\ln Z_G(\mu, V, \beta) &= - E d\beta + \beta pdV + N d\beta\mu \end{align*}

Isothermal-isobaric ensemble

Your browser does not support SVG
\begin{align*} {\mathcal P}(V,E) &\propto \Omega(V,E;V_{\rm tot},E_{\rm tot}) \\ \Omega(V,E;V_{\rm tot},E_{\rm tot}) &= \Omega(V,E) \Omega_B(V_{\rm tot}-V,E_{\rm tot}-E) \end{align*}

Isothermal-isobaric ensemble

  • Boltmann distribution

    \begin{align*} P(N,V,E) &= \frac{\Omega(N,V,E)}{\Delta(N,\beta p,\beta)} e^{\beta p V - \beta E} \end{align*}

  • partition function

    \begin{align*} \Delta(N,\beta p,\beta) &= \sum_{V,E} \Omega(N,V,E)\,e^{\beta p V - \beta E} \end{align*}

  • free energy

    \begin{align*} \beta G(N,p,T) &= - \ln\Delta(N,\beta p,\beta) \end{align*}
    \begin{align*} dG &= - SdT + Vdp + \mu dN \\ d \ln\Delta(N,\beta p, \beta) &= - E d\beta + V d(\beta p) + \beta \mu dN \end{align*}

Simple fluids

  • \(N\) spherical atoms of mass \(m\)
  • position of atom \(\alpha\) is \({\bf r}_\alpha\)
  • momentum of atom \(\alpha\) is \({\bf p}_\alpha\)
  • point in phase space: \({\boldsymbol\Gamma}=({\bf r}_1,\dots{\bf r}_N,{\bf p}_1,\dots,{\bf p}_N)\)
  • pairwise additive potential \(u(|{\bf r}_\alpha-{\bf r}_{\alpha'}|)\)

  • Hamiltonian: \(H({\boldsymbol\Gamma})=U({\bf r}_1,\dots{\bf r}_N)+K({\bf p}_1,\dots,{\bf p}_N)\)

    \begin{align*} U({\bf r}_1,\dots{\bf r}_N) &= \frac{1}{2} \sum_{\alpha\ne\alpha'} u(|{\bf r}_\alpha-{\bf r}_{\alpha'}|) \\ K({\bf p}_1,\dots,{\bf p}_N) &= \sum_\alpha \frac{p_\alpha^2}{2m} \end{align*}

Fluid structure

  • The $n$-particle density \(\rho^{(n)}({\bf r}_1,\dots,{\bf r}_n)\) is defined as \(N!/(N-n)!\) times the probability of finding \(n\) particles in the element \(d{\bf r}_1\cdots d{\bf r}_n\) of coordinate space.

    \begin{align*} &\rho^{(n)}({\bf r}_1,\dots,{\bf r}_n) = \frac{N!}{(N-n)!} \frac{1}{Z(N,V,T)} \int d{\bf r}_{n+1}\cdots d{\bf r}_N\, e^{-\beta U({\bf r}_1,\dots,{\bf r}_N)} \\ &\int d{\bf r}_1\cdots d{\bf r}_n\,\rho^{(n)}({\bf r}_1,\dots,{\bf r}_n) = \frac{N!}{(N-n)!} \end{align*}

  • This normalization means that, for a homogeneous system, \(\rho^{(1)}({\bf r})=\rho=N/V\)

    \begin{align*} &\int d{\bf r}\, \rho^{(1)}({\bf r}) = N \qquad \longrightarrow \qquad \rho V = N \\ &\int d{\bf r}_1d{\bf r}_2\, \rho^{(2)}({\bf r}_1,{\bf r}_2) = N(N-1) \end{align*}

n-particle correlation function

  • The $n$-particle distribution function \(g^{(n)}({\bf r}_1,\dots,{\bf r}_n)\) is defined as

    \begin{align*} g^{(n)}({\bf r}_1,\dots,{\bf r}_n) &=\frac{\rho^{(n)}({\bf r}_1,\dots,{\bf r}_n)} {\prod_{k=1}^n \rho^{(1)}({\bf r}_i)} \\ g^{(n)}({\bf r}_1,\dots,{\bf r}_n) &= \rho^{-n} \rho^{(n)}({\bf r}_1,\dots,{\bf r}_n) \qquad \mbox{for a homogeneous system} \end{align*}

  • For an ideal gas (i.e., \(U=0\)):

    \begin{align*} &\rho^{(n)}({\bf r}_1,\dots,{\bf r}_n) = \frac{N!}{(N-n)!} \frac{\int d{\bf r}_{n+1}\cdots d{\bf r}_N}{\int d{\bf r}_{1}\cdots d{\bf r}_N} = \frac{N!}{(N-n)!} \frac{V^{N-n}}{V^N} \approx \rho^n \\ &g^{(n)}({\bf r}_1,\dots,{\bf r}_n) \approx 1 \\ &g^{(2)}({\bf r}_1,{\bf r}_2) = 1 - \frac{1}{N} \end{align*}

radial distribution function

  • \(n=2\): pair density and pair distribution function in a homogeneous fluid

    \begin{align*} g^{(2)}({\bf r}_1,{\bf r}_2) &= \rho^{-2} \rho^{(2)}({\bf r}_1,{\bf r}_2) \\ g^{(2)}({\bf 0},{\bf r}_2-{\bf r}_1) &= \rho^{-2} \rho^{(2)}({\bf 0},{\bf r}_2-{\bf r}_1) \end{align*}

  • Average density of particles at r given that a tagged particle is at the origin is

    \begin{equation*} \rho^{-1} \rho^{(2)}({\bf 0},{\bf r}) = \rho g^{(2)}({\bf 0},{\bf r}) \end{equation*}

  • The pair distribution function in a homogeneous and isotropic fluid is the radial distribution function \(g(r)\),

    \begin{equation*} g(r) = g^{(2)}({\bf r}_1,{\bf r}_2) \end{equation*}

    where \(r = |{\bf r}_1-{\bf r}_2|\)

radial distribution function

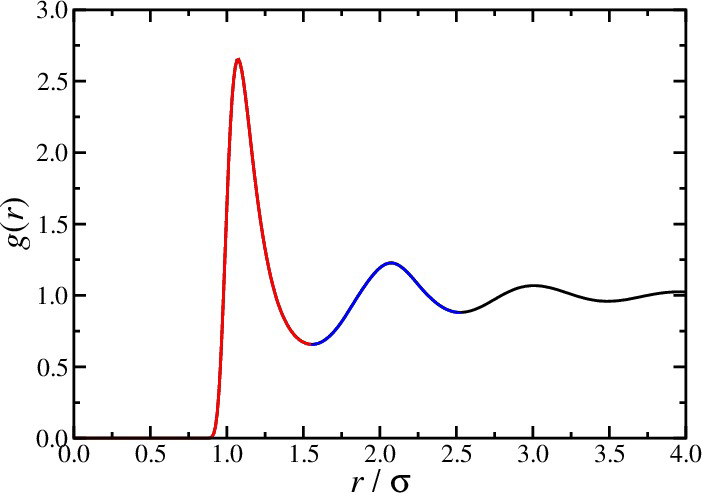
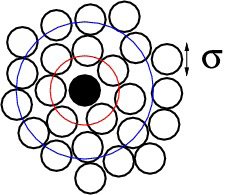
radial distribution function

  • Energy

    \begin{align*} U &= N \rho \int d{\bf r} u(r) g(r) \end{align*}

  • virial equation

    \begin{align*} \\ \frac{\beta p}{\rho} &= 1 - \frac{\beta\rho}{6} \int d{\bf r} w(r) g(r) \end{align*}

  • compressibility equation

    \begin{align*} \rho k_BT \kappa_T &= 1 + \rho \int d{\bf r} [g(r)-1] \end{align*}

structure factor

  • Fourier component \(\hat{\rho}({\bf k})\) of the instantaneous single-particle density
\begin{align*} \rho({\bf r}) &= \sum_\alpha \delta^d({\bf r}-{\bf r}_\alpha) = \int \frac{d{\bf k}}{(2\pi)^d} \hat{\rho}({\bf k}) e^{-i{\bf k}\cdot{\bf r}} \\ \hat{\rho}({\bf k}) &= \int d{\bf r} \rho({\bf r}) e^{i{\bf k}\cdot{\bf r}} \end{align*}
  • Autocorrelation function is called the structure factor \(S(k)\)
\begin{align*} \frac{1}{N}\langle\hat{\rho}({\bf k})\hat{\rho}(-{\bf k})\rangle &= 1 + \frac{1}{N}\left\lt \sum_{\alpha\ne\alpha'} e^{-i{\bf k}\cdot({\bf r}_\alpha-{\bf r}_{\alpha'})} \right\gt \\ S({\bf k}) &= 1 + \rho\int d{\bf r}[g({\bf r})-1] e^{-i{\bf k}\cdot{\bf r}} \end{align*}
  • \(S({\bf k})\) reflects density fluctuations and dictates scattering

Fourier decomposition

Consider the function

\begin{align*} f(x) &= x^2 + \frac{1}{2}\sin 6\pi x + 0.1 \cos 28\pi x \end{align*}

Fourier representation:

\begin{align*} f(x) &= \sum_{n=0} A_n e^{-i k_n x} \end{align*}

where \(k_n = 2\pi n\).

Fourier decomposition

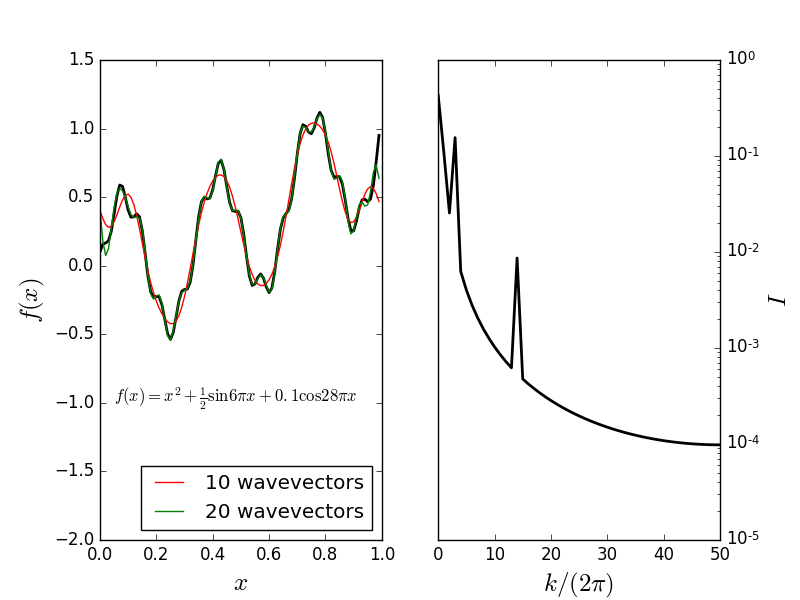
Structure factor

  • A peak at wavevector \(k\) signals density inhomogeneities on the length scale \(2\pi/k\)

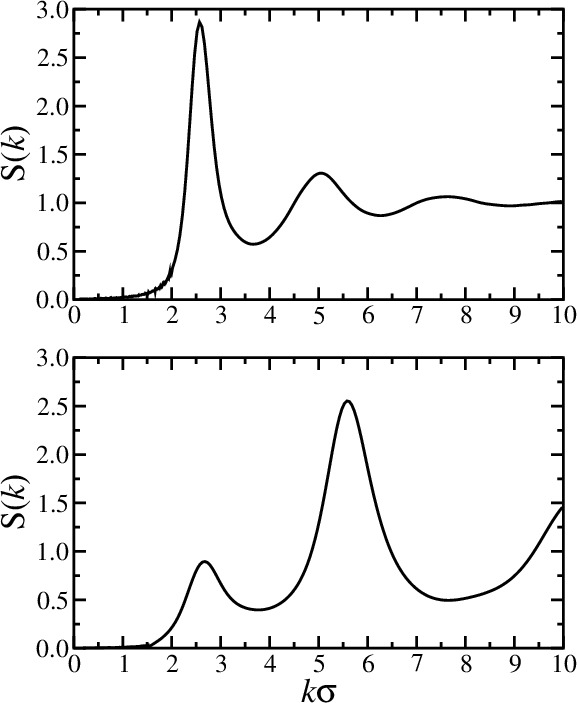
  • \(k=0\) limit is related to the isothermal compressibility \(\kappa_T\)
\begin{align*} \hat{S}(0) &= 1 + \rho \int d{\bf r}\, [g(r)-1] = \rho k_B T \kappa_T \end{align*}

Further reading

  • D Chandler, Introduction to Modern Statistical Mechanics (1987).
  • DA McQuarrie, Statistical Mechanics (2000).
  • LE Reichl, A Modern Course in Statistical Physics (2009).
  • JP Hansen and IR McDonald, Theory of Simple Liquids, 3ed (2006).

Questions?